I’m now 99% Confident in ubench.h
So I recently created a new single header C/C++ library for benchmarking your code - ubench.h.
It’s funny how as soon as you push something public you realise all the flaws in it - but that’s fine! Software (like people) should grow and develop as it gets older.
The way I was trying to gauge the accuracy of the result from multiple benchmark runs was somewhat… broken. In this PR I’ve switched to using a confidence interval, and I’ll now explain why.
The Broken Approach⌗
So I’ve never studied statistics in any capacity. I’d always followed the believe that statisticians were like demi-lawyers - good at manipulating the same set of ‘facts’ to tell whatever story they want.
But ever since I watched the rather awesome Elan Ruskin talk about statistical tests for games I realised I needed to level up.
So the first thing I learned about was standard deviation - well really I had to re-learn this because I’m pretty certain I got taught it in high school and immediately forgot it… For those uninitiated the standard deviation gives you a measure of how variable the average of a set of data is. Let’s say you’ve got 10 recordings of something - the average is just the sum of all items divided by the number of recordings, otherwise know as the mean.
You then use this mean, subtract it from each of the original values, square them, divide by the number of iterations and then take the sqrt of that:
ubench_int64_t ns[iterations];
ubench_int64_t avg_ns = 0;
for (i = 0; i < iterations; i++) {
avg_ns += ns[i];
}
avg_ns /= iterations;
for (i = 0; i < iterations; i++) {
const double v = ns[i] - avg_ns;
deviation += v * v;
}
deviation = sqrt(deviation / iterations);
Once I had this I then used the standard deviation to measure how variable the result was. A high standard deviation means that you don’t have confidence that the result you’ve recorded is stable enough to be meaningful. Conversely a low standard deviation makes you confident. Previously I was aiming for a standard deviation below 2.5% as a gauge of how good the result was.
The problem is that getting a standard deviation below a low margin across many different types of machines we test on (laptops, desktops, mobiles, consoles, etc) can be quite difficult. Pre-emption of the running thread might cause a temporary spike in a given tests result, or you might get a very fast run that hits no speed bumps and thus runs really fast. These outlier results can really affect the standard deviation of the result.
Since I didn’t know much about stats I wrongly thought that the best way to cut out the occassional high variance results was to just sort all the runs and then slice off the top and bottom N items:
ubench_int64_t ns[iterations];
ubench_int64_t avg_ns = 0;
// Sort the results.
qsort(ns, iterations, sizeof(ubench_int64_t), ubench_sort_func);
for (i = 1; i < (iterations - 1); i++) {
avg_ns += ns[i];
}
avg_ns /= (iterations - 2);
for (i = 1; i < (iterations - 1); i++) {
const double v = ns[i] - avg_ns;
deviation += v * v;
}
deviation = sqrt(deviation / (iterations - 2));
This would cut off the top and bottom worse skewed results. The problem is that this didn’t really reduce the standard deviation that much in the first place, and secondly it discounted valuable collected data.
Another problem with the standard deviation is that its not necessarily true that collecting more data will reduce the deviation itself - just because you are collecting more data doesn’t meant that the data will be any less deviant.
So I needed another approach.
I’m 99% Confident with my Interval⌗
If we look at the typical spread of data for any measurement, the data tends to centre around the average or mean value. This is called the normal distribution or a bell curve, and generally looks like:
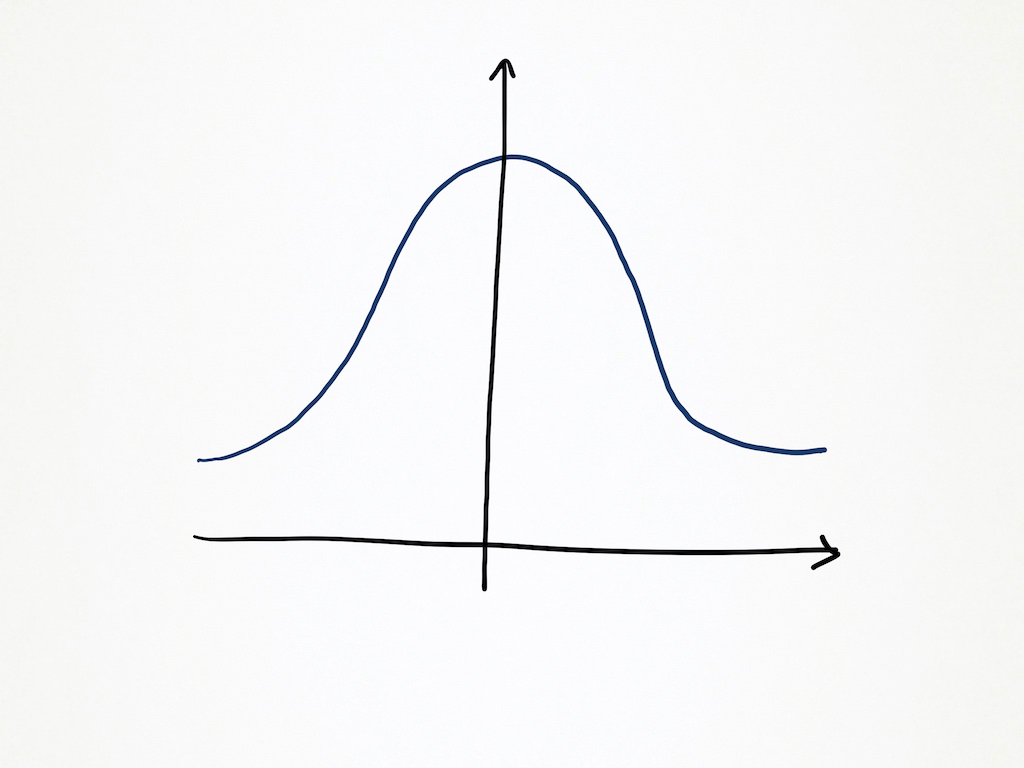
In this chart, x = 0 is the the average, and y is the number of samples that matched the given value of x. This is what data tends to look like from benchmarks. We can see that most of the samples (larger y) occurs closer to the mean, and there is less and less the further we go away. Given I want to cut out any outliers large or small, what we really want is a way to say ‘Is most of the data close enough to the average?’.
Luckily some people smarter than me have a way to do this - and it is called a confidence interval. A confidence interval is a way to say ‘If we only care about X% of the data, how close is that to the average?’. For my use case I’m using a 99% confidence interval - EG. I’m asking the stats to give me a number for how close the 99% of the samples that are closest to the average actually are:
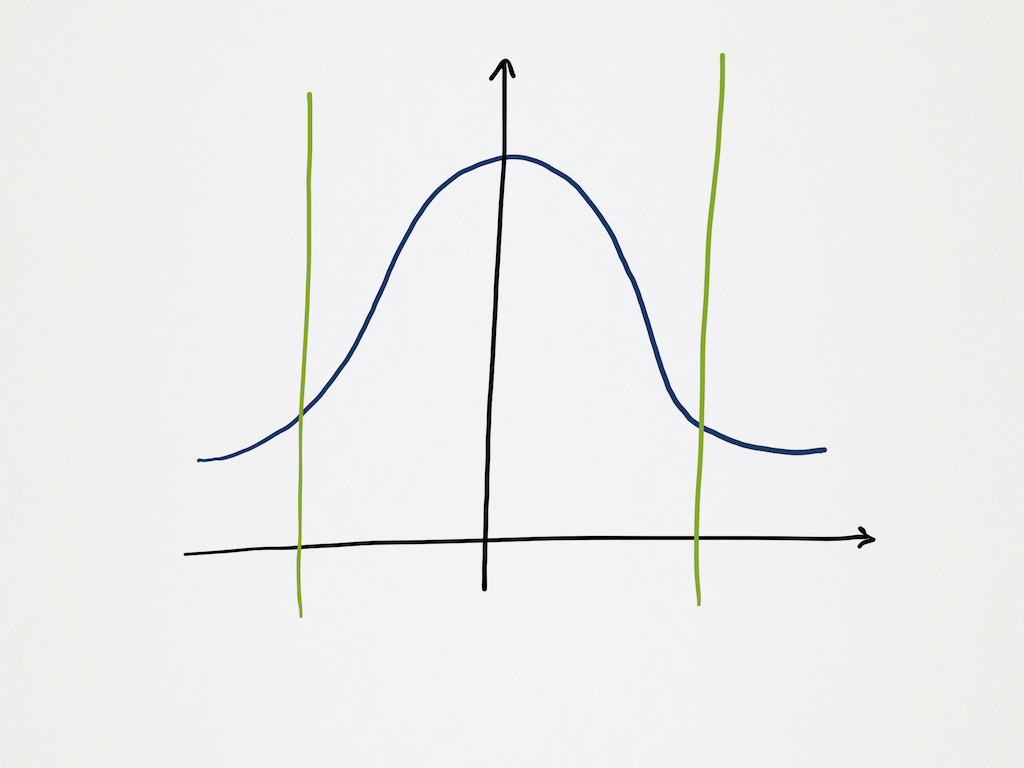
We can see in this chart the two extra lines - this is my confidence interval, I’m only wanting to know how close the X% of the values that are occuring within these bounds are to the average.
Calculating a confidence interval is pretty easy too:
for (i = 0; i < iterations; i++) {
avg_ns += ns[i];
}
avg_ns /= iterations;
for (i = 0; i < iterations; i++) {
const double v = ns[i] - avg_ns;
deviation += v * v;
}
deviation = sqrt(deviation / iterations);
// Confidence is the 99% confidence index - whose magic value is 2.576.
confidence = 2.576 * deviation / sqrt(iterations);
Now there is this magic constant 2.576 - I genuinely have no idea where it
comes from or why it is what it is. But
some smart stats people
has done some math stats stuff and… this is the value I need.
Now instead of aiming for a 2.5% range with my botched standard deviation, I instead look for a 2.5% range with my 99% confidence interval instead. The great thing about the confidence interval is the more data you throw at it the lower it goes. I think this is because you cut out more outliers (the 1%) the more samples you have, but whatever the reason it means that if I haven’t achieved the 2.5% range I want I can just re-run it with more samples and that generally does what I want. Nice!
The output from ubench.h has now changed to display the confidence interval too, and I added a request from @zeuxcg to change the displayed timing in ms/s/us where appropriate - which makes it much more legible:
[ RUN ] cpp_my_fixture.strchr
[ OK ] cpp_my_fixture.strchr (mean 4.115ms, confidence interval +- 2.039480%)
[ RUN ] cpp_my_fixture.strrchr
[ OK ] cpp_my_fixture.strrchr (mean 57.057ms, confidence interval +- 0.445810%)
Conclusion⌗
So I’ve made ubench.h more consistent at profiling and actually used real mathematically sound statistics rather than my bodged attempt at it - nice! For my users it’ll mean more consistent data and more confidence (har har) that it is doing the right thing.